
こんにちは!
今回は、F検定(Fけんてい)についてわかりやすく解説します。
「分散を比べる検定」と聞くと一瞬で眠くなる人も多いと思いますが、
今回は身近な例と計算つきで、面白く学べる内容にしました!
そもそもF検定ってなに?
F検定は、2つのグループのデータの「ばらつき(分散)」が同じかどうかを調べる検定です。
たとえば
AクラスとBクラスで、数学のテストの点数にばらつきの差があるか?
機械Aと機械Bが作る部品の精度に違いがあるか?
など、「どっちが安定している(=分散が小さい)?」を調べたいときに使います。
事例:A班とB班で部品の精度に差があるか?
ある工場で、A班とB班が同じ部品を作っています。
それぞれの班で5つずつ部品を測定してみました。
| A班の長さ(mm) | 100.2 | 100.4 | 100.3 | 100.1 | 100.0 |
|---|---|---|---|---|---|
| B班の長さ(mm) | 100.0 | 100.5 | 100.8 | 100.3 | 100.4 |
目で見ると、B班の方がばらついていそうです。
これを「感覚」ではなく「数式」で確かめてみましょう!
Step1:分散を求めよう
まずは、それぞれの班の分散を計算します。
A班の平均

実際に計算をしてみよう
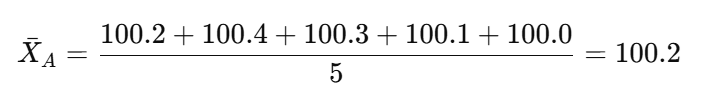
A班の分散

実際に計算してみよう
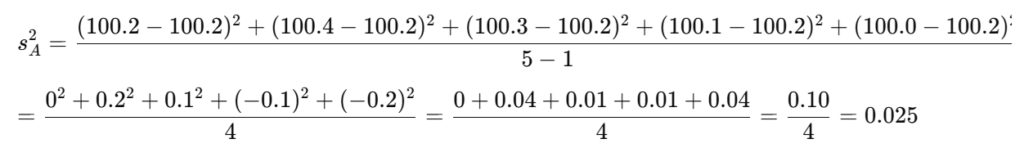
B班の平均

実際に計算してみよう
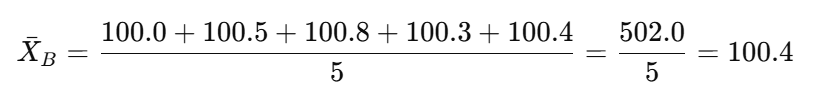
B班の分散

実際に計算してみよう
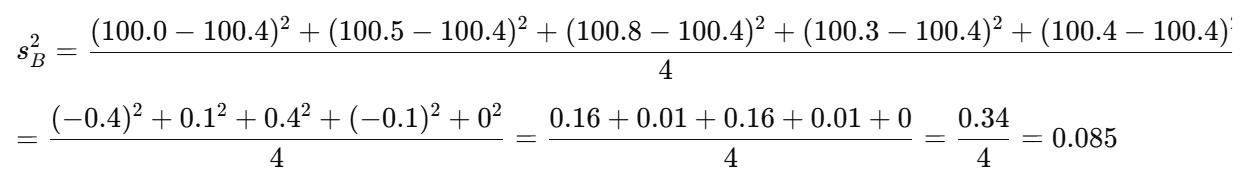
Step2:F値を求める
F検定では、大きい方の分散 ÷ 小さい方の分散を計算します。
F=0.0850.025=3.4F = \frac{0.085}{0.025} = 3.4
Step3:F分布表で「有意差」があるかを確認
F値が「偶然とは思えないほど大きいか」を判断するには、**F分布表(自由度)**を見ます。
今回は、
A班の自由度:5 – 1 = 4
B班の自由度:5 – 1 = 4
有意水準(よく使う5%)でのFの基準値 ≒ 6.39(F(4,4))
となります。
結論:
計算したF値 = 3.4
F分布表の基準値 = 6.39
3.4 < 6.39 → 有意差なし
最終的な判断:分散に差は「ない」と考えられる
A班とB班のばらつきに明確な差はないということになります。
つまり、「どちらの班も同じくらい安定して作業している」と言えそうですね!
補足:なぜ「分散の比」なの?
F検定の「F」は、**Fisher(フィッシャー)**という統計学者の名前が由来。
彼は、「分散の比にはF分布という分布がある」と見つけました。
この検定のおかげで、「感覚的なばらつきの違い」を数値で証明できるようになったのです。
まとめ
| ポイント | 内容 |
|---|---|
| 検定の目的 | 2つのグループの分散に差があるかを調べる |
| 計算方法 | 大きい分散 ÷ 小さい分散 |
| 判断方法 | F分布表と比べて、有意差があるか判断 |
おまけ:F検定はどんなときに使う?
t検定の前に、「分散が等しいか」を調べたいとき
製品の品質安定性を比較したいとき
実験での測定誤差を比べたいとき
など、F検定は地味だけど超重要な検定です!

「分散」とか「検定」とか聞くと難しそうですが、
実際には「ばらつきに差があるか」を確認するだけです。



コメント